House 11A

HOUSE 11A, 1978
16mm Cel Animation
This project was initiated as a response to the sequential diagrams employed by the architect Peter Eisenman to illustrate the role of process in his architecture.
HOUSE 11A had been commissioned by curator and scholar Kurt Forster who stipulated that the house be modeled upon a Klein Bottle, an impossible topological figure with no inside and no outside. Peter posed the question: How can we represent this object as it was conceived; as a void imploding a solid (above ground) and a solid imploding a void (below ground)?
I had experience with conventional cel animation and an interest in topological figures and offered to animate a sequence of Eisenman’s axonometric drawings piercing a plane. Animation was an unlikely medium for architectural renderings in 1978, but I felt that House 11A was particularly suited to filmic representation as it had been conceived of as the formal evolution of continuously distroted two-dimensional surfaces. I approached the project with cel and an x-acto knife; copying the axonometric drawings that had been rendered with rapidograph on vellum with Pantone sheets and tape on cel. I shot the sequences on a conventional Oxberry animation stand to make a short 16mm demonstration. The intention was to use the piece as a proof of concept to support efforts to make the longer film. The subtitle, A Documentary in which El Solid Meets La Void, speaks to the spirit of the Institute during that period as well as to the sense of architectural form inhabiting multiple narratives.
CLIENT’S STATEMENT
Kurt Forster, 1978
As the client, I would like to remain a viewer of the house while inside of it. I think that most architecture leaves you with a sense of being isolated in one compartment or fragment of it. It forces you to close the door on the rest of it. The only connections that remain are those of the most elementary and literal kind, namely function. For the first time, in thinking of a house in the conceptual sense, the house I am going to live in, I ask myself, why would I be inside the house, what would I do inside the house? I think I would like to be inside the house, apart from all the obvious reasons, in order to constantly reconstitute the world outside. So therefore I would be a viewer who is inside, separate from what he is dealing with, which is the world short and simple on the outside, and at the same time, while I am inside and separated from it, I would be able to know about it, I would have the world present. I would like to be in this dual condition of the viewer who is both inside and outside of the house.
In other words, traditionally we are used to perceiving houses as unitary from the outside and disintegrating into shut-off parts inside. The public image of integral unity tends to be that of a mask drawn over the internal reality of the house. I would like to think that it is possible to modify this situation in such a way as to neutralize the exterior and represent the connections and separations among the parts inside. The internal distribution would offer a visitor’s approach from within an occupant’s view from without. It might even be possible to go beyond these traditional opposites and define, in turn, both their relatedness and their difference – based not only on their use but also on the conditions of life in a larger sense.
And on a smaller scale, the people who live in a house are separate entities themselves, they reproduced the state of the world outside, and sometimes, when they go out into it, they become like and are apart. But inside the house they are also together. To simply reaffirm their separateness from the world would be to fall back on the oldest of cliches, the house as nest; the inside of the house would remain undivided and no new question addressed. But the real question is, when the members of the family come back into the house are they together or separate, both from each other and from the world.
ARCHITECT’S STATEMENT
Peter Eisenman, 1978
It has become clear in this century that Euclidean geometry is no longer fully capable of expressing the uncertainty and relativity of the modern world, the changed relationship of man and the objects around him. Topological geometry, on the other hand, which has to do with indeterminate distances and infinitely unbroken surfaces which are conceptually invertebrate, seems to approximate the condition more closely. A Mobius strip, for example, is an invention of topological geometry. It is a plane which, when folded, produces a line along its edges which is simultaneously on the inside and outside of that plane. A Klein bottle is the same idea in three dimensions.
This house is a folded membrane; the EL approximates the unbroken and continuous surface of the Klein bottle, while at the same time suggesting an architectonic condition of inside and outside. In Euclidean terms, the EL is also a fragmentary condition. It is both moving toward completion as a pure Euclidean cube and moving toward dissolution from it. It is the essential fragment; complete in itself, yet asymmetrical, unstable, at once becoming and disappearing.
The architectural condition is conceptualized as two topological sheets; both exhibit qualities of permeability and distortion. The horizontal layers are distorted by the vertical energy, which imprints the white layer on the ground and the brown layer on the air. The resulting configuration appears to have an inside and an outside but in fact there is no real inside and no real outside, only two deformed membranes.
The initial deforming agents are a series of three-dimensional EL molds. These are the specific, thickened deformation of the topological sheets which are conceived of as impacting the initial surfaces from the opposite quadrants, imprinting and distorting the topological sheet.
As all the of the interior wall surfaces which partake of the whole are neither inside nor outside, the same condition accrues to the outside where one feels literally that one is inside.
The house is an attempt to conceive of an other condition of object; not a formal, arbitrary, representational sign, not a sign of itself; and not an abstraction, which is merely a less obvious form of representation, but rather a sign which is only an approximation which in itself seems to disappear, leaving only the sense of that condition which it is approximating.
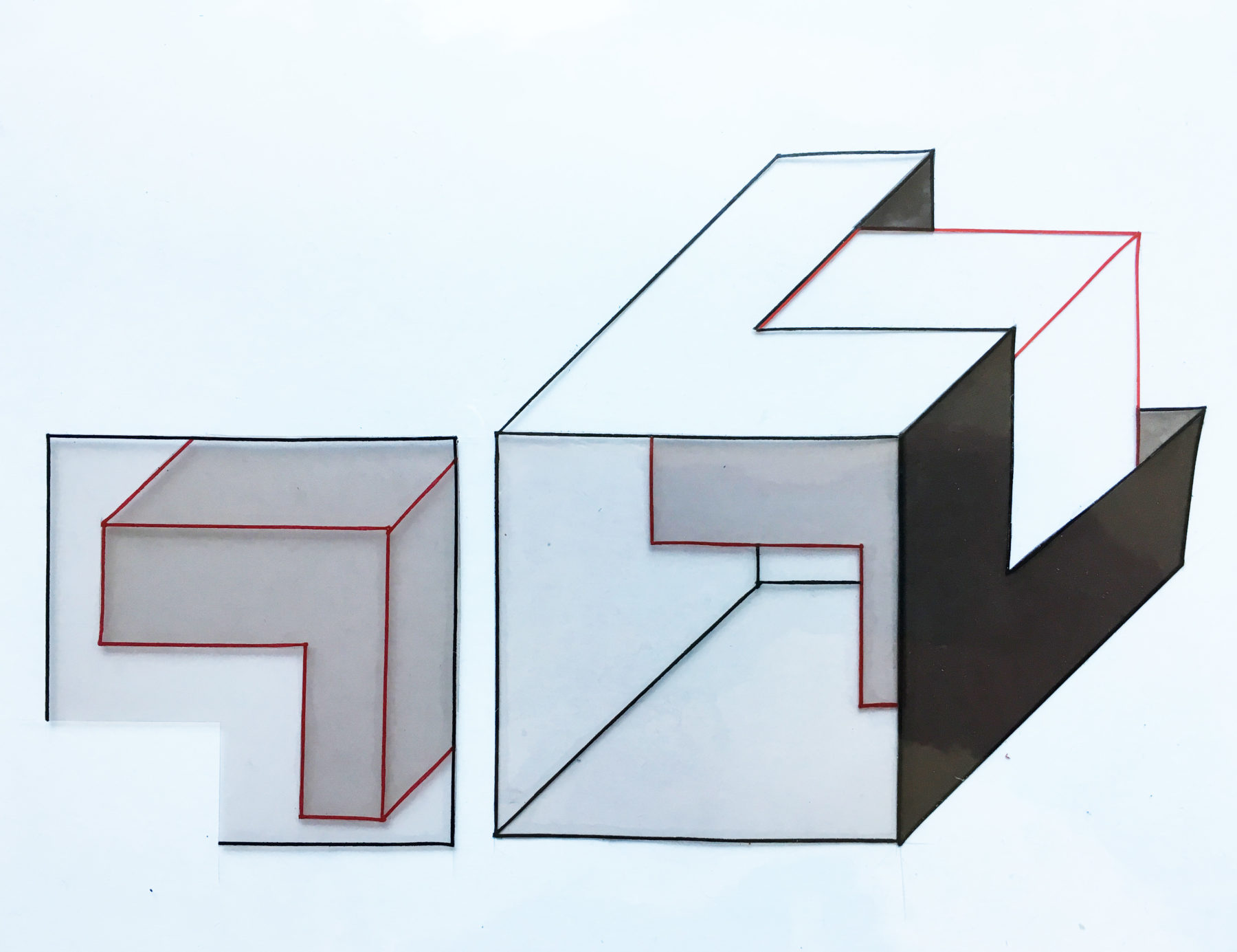
Cel Detail, HOUSE 11A 1978
FILMMAKER’S STATEMENT
Peggy Weil , 1978
The concerns of the film reflect the commitment of the client and of the architect towards a redefinition of the traditional notions of object. House 11A threatens to reconcile the (traditionally) irreconcilable, inside with outside. The film aims to achieve a resolution between the dual condition of film; as a still moving picture and as a series of still pictures that move and between the diagrammatic content and the overall structure.
The house evolves from continuously folded sheets. The film unfolds as a series of animated diagrams describing the formation of the house; incidents of transition and equilibrium among earth and sky, solid and void, progressively (de)forming the conceptualized sheets.
The predominant shape of the house is the EL, suggested by the Klein bottle. The (two-dimensional) film takes its overall shape from the Mobius strip, not literally as a twisted loop of film, but rhythmically. The fold is embodied in the order of the film, its basic measure an expression of the progression of a line extended in opposing directions along the one side of a Mobius strip.
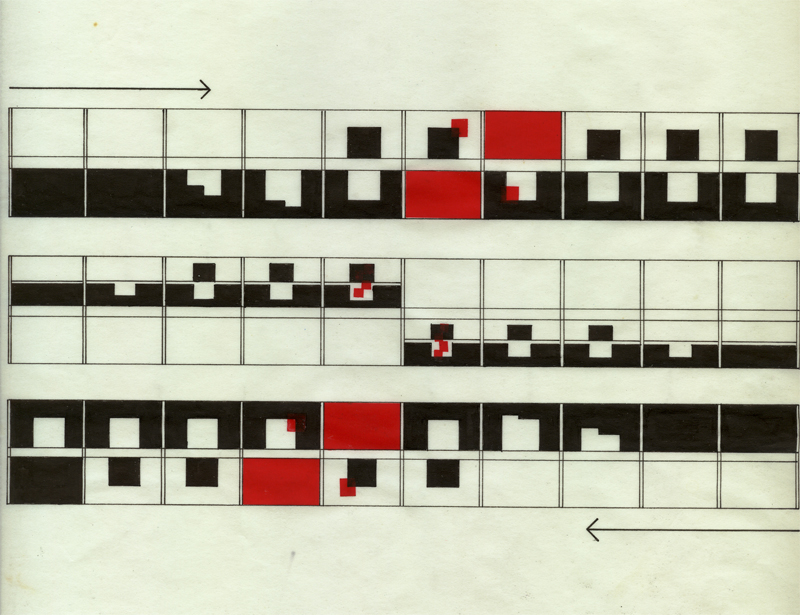
Score, HOUSE 11A 1978